Skip to main content

The basic concepts of deep neural networks

We will explore 3 basic concepts of deep neural networks. The first part will explain how back-propagation algorithm works. The second talks about softmax function. And the last one is cost function.
Inside Backpropagation algorithm
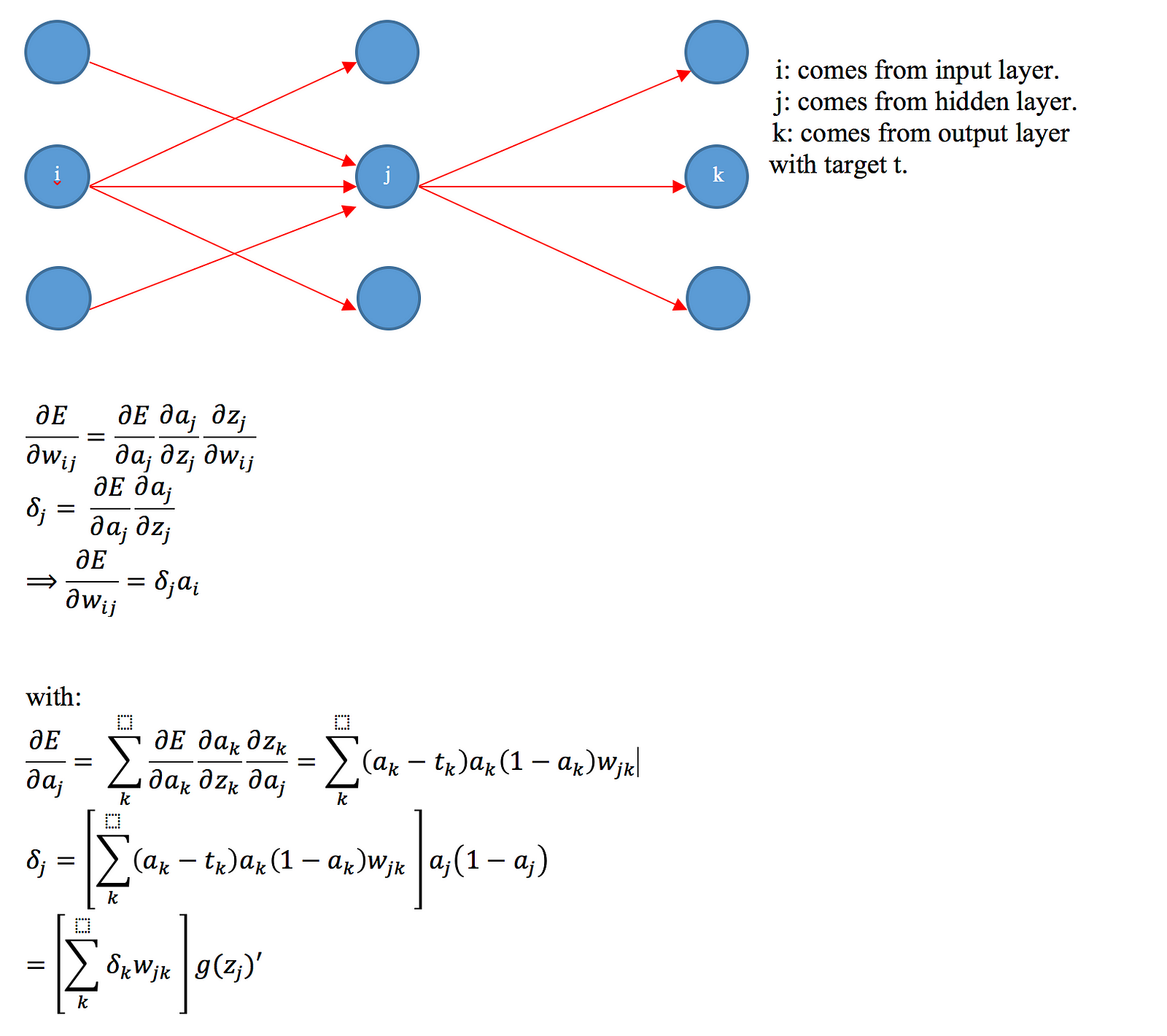
The main idea of Backpropagation algorithm is aims to minimize the overall neural network error. To do that, we find out the partial derivative of error and weight vector. Take a look in a simple Neural Network:
From Sigmoid function to Softmax function and Cross-entropy cost function
In the classification problem with multinomial distribution, how do we know which label is choosen? Softmax function is used to do that. In practice, some people might also use one2All mechanism to detect label by traning many logistic regression models. However, it is not effective solution. Softmax function helps us to determine the label also we can calculate the cost from this easily by using Cross-entropy cost function.
Sigmoid function
Sigmoid function comes from binomial distribution model. There are only label 0 or label 1 occur. In order to train a logistic regression model, we find the weights that maximize the likelihood of the model (log is concave function):

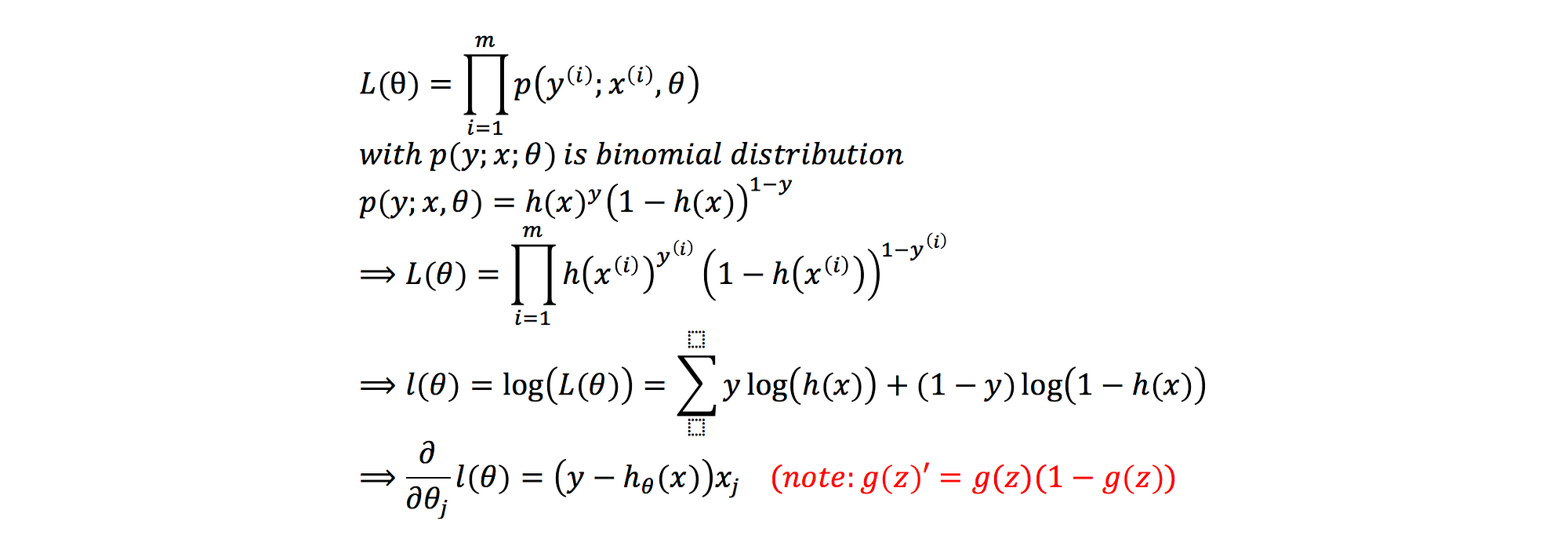
This therefore gives us the stochastic gradient ascent (log is concave function) rule:
It means, we pick the parameter that makes the observed data x most likely with when assuming output y =1.
Sigmoid function and Cross entropy cost function
Now, we have k labels instead of 2 labels in logistic regression. Let’s see how we chose the best one from k. Remind that the generalized linear model is defined in formal like this: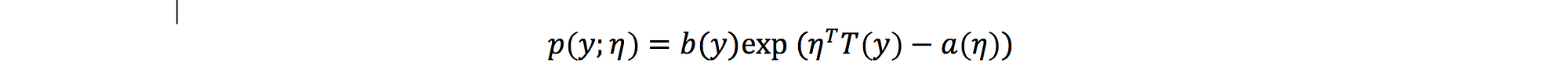
With multinomial distribution model, We define a vector y with k factors to determine a label is choosen or not.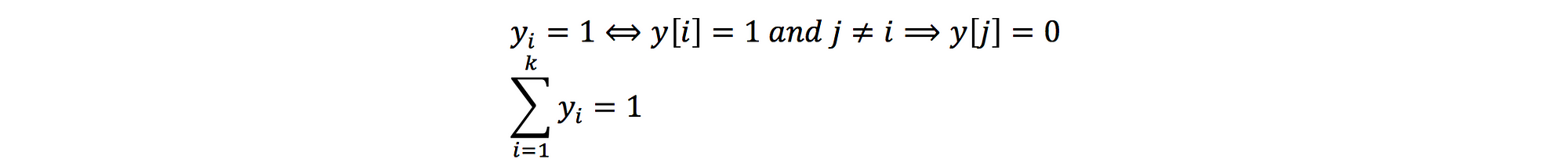
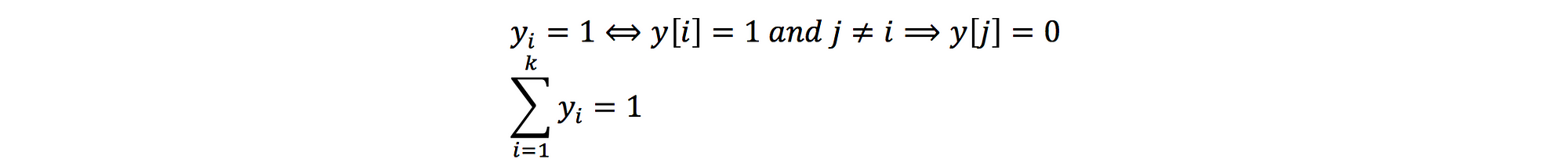
We have of probabilities of labels:
The probability density function or likelihood: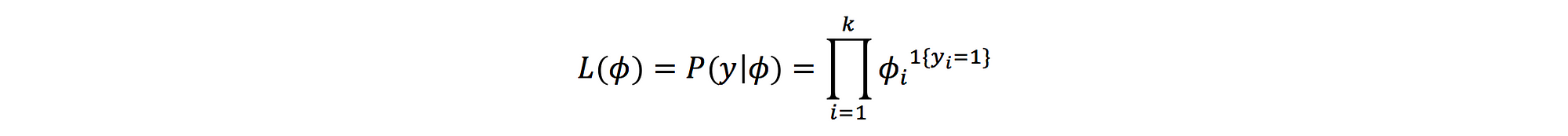
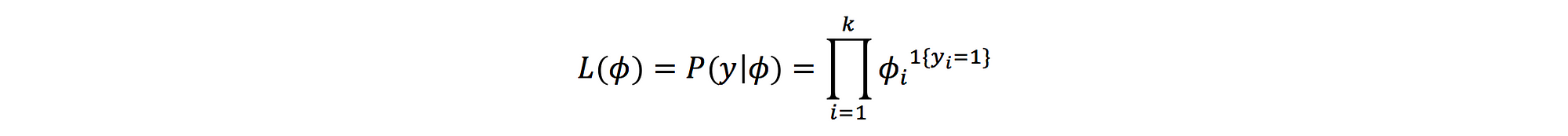
log likelihood: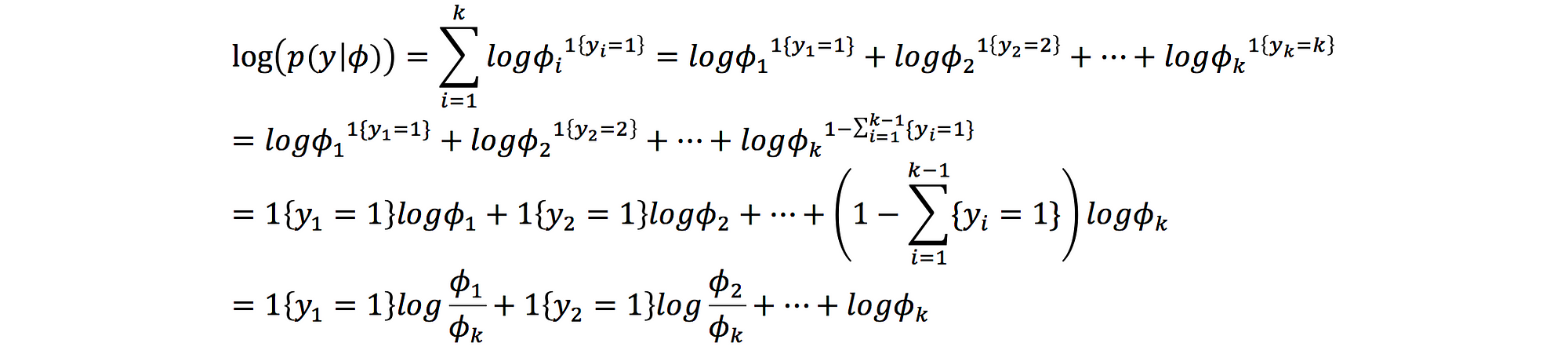
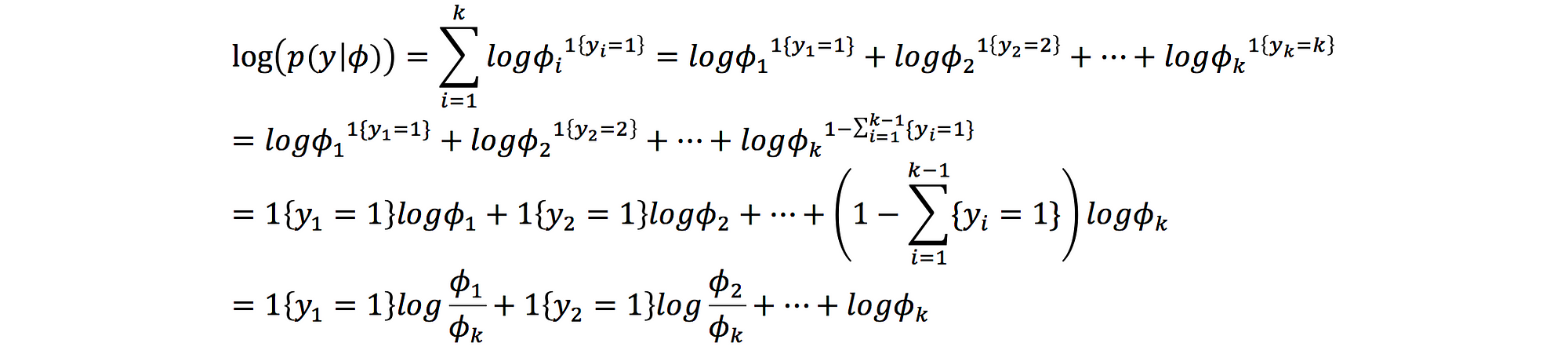
we assume that: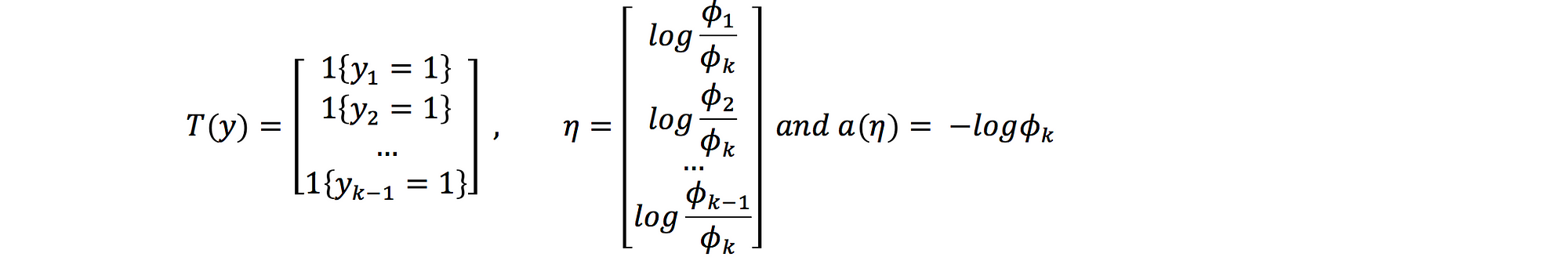
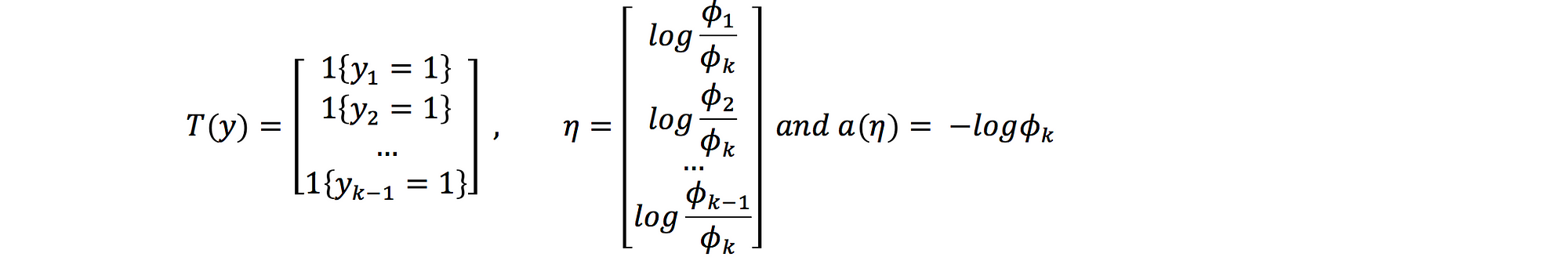
And reference to generalized linear model, we will have: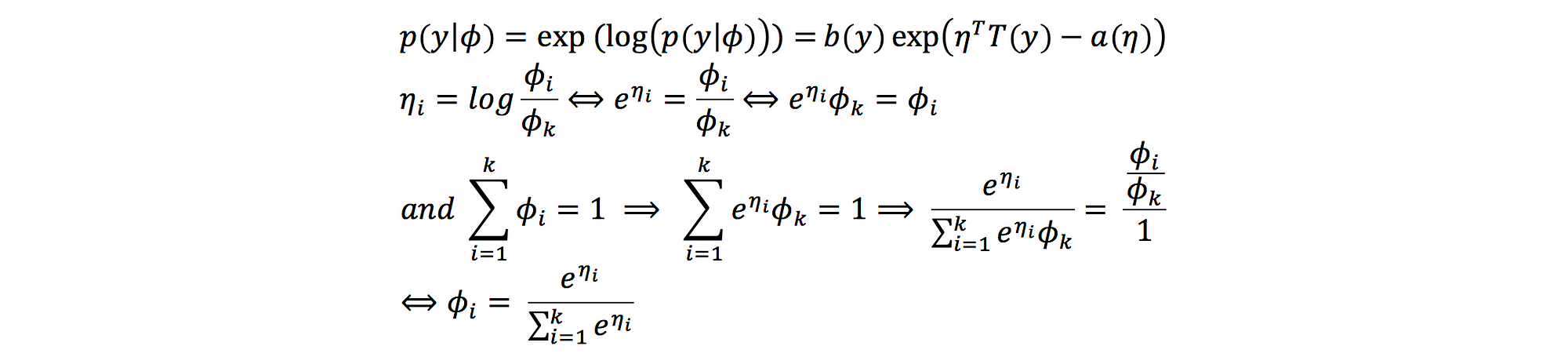
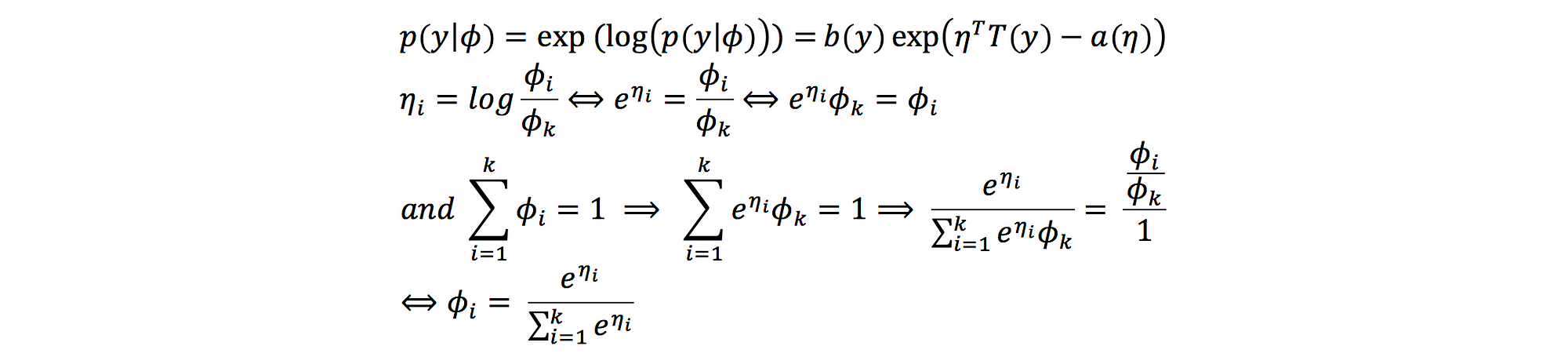
And the cost function: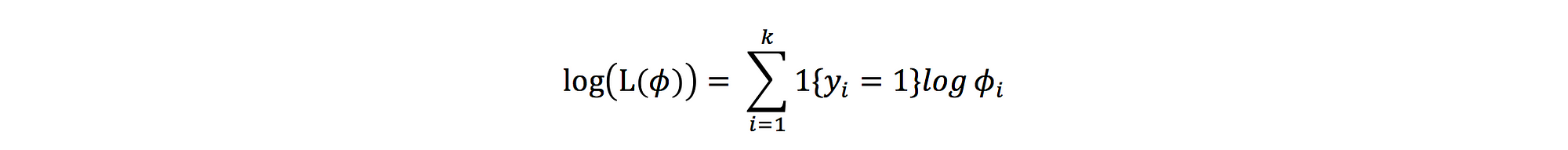
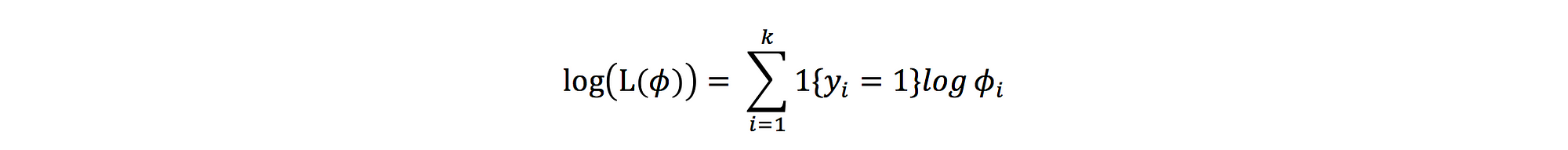
Sometimes, we see the similar one: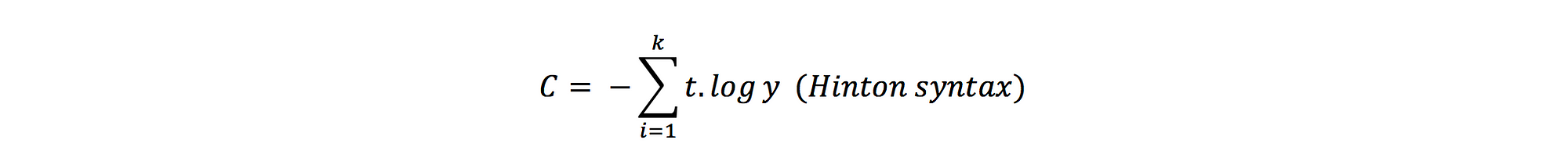
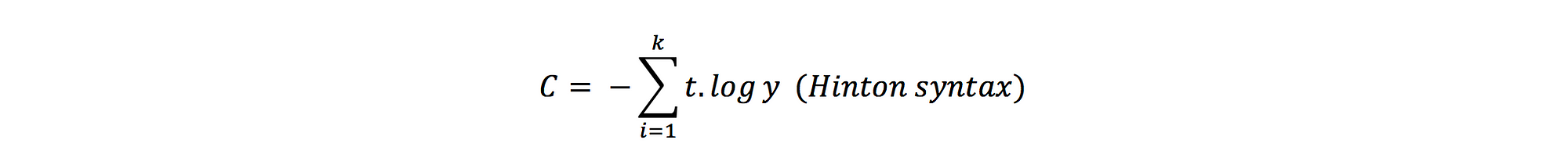
These points here are what I have learned and think they are fundamental and basic of a deep neural network.
Labels:

Comments

Post a Comment

Popular posts from this blog

Generative Adversarial Networks

Generative Adversarial Networks (GAN) is one a Neural Network architecture which simulates zero-sum game. There are 2 parts of this Neural Network. The first is called Generator and other is called Discriminator. Generator tries to mimic data and make the fake data likes the real data in distribution. Meanwhile, the Discriminator tries to maximize the difference between real data and fake data. It is reason we call zero-sum game. Two parts are coaction with each other. This structure makes the GAN to be a interesting Neural Network architecture and it has many application in both academic and industry. In modeling, the GAN is an approach of equilibrium Networks such as Boltzmann Machine did. It is an optimization problem with objectives of: minimize Generator and maximum Discriminator simultaneously.  $max_{D}min_{G} V(D,G)$  $max_{D}min_{G} V(D,G) = E_{x\sim p_{data}(x)}[log(D(x))] + E_{z\sim p_{z}(z)}[log(1 - D(G(z)))]$ $V(D,G)$ is optimization problem subject to G ...
Post a Comment
Read more

Mutual information and feature selection

   Feature selection is one of the most important step to make your model works well. In data mining, feature selection is the first step and it effects to all of process. Feature selection help model on some points: - The model will be trained faster - Reduce overfitting - Simplifying model - Reduce the dimension of data Hence, feature selection is kick-off step and it effects overall, especially in model. There are 3 type of feature selection: Filter methods, wrapper methods and embedded methods. Filter methods: this methods "filter" data based on correlation score. Normally, our data have many features, and a label. We calculate the correlations between features and label. After that, we only retrain the features that have a good (relevant) correlated score and remove others. In this type of method we have some ways to calculate the correlation. - Pearson correlation: this one is based on covariance between 2 continuous variables. $$ p_{X,Y} = \frac {Cov(X, Y)...
Post a Comment
Read more